Lab 3: Evaluators

Overview

The goal of this lab is to develop the concepts we saw in class on Monday, culminating in a working and usable evaluator for the lambda calculus.

There is quite a bit of code in this week’s lab, but don’t get distracted by it! The main things to take away are:

Understanding the differences between call-by-name and call-by-value.
Writing Haskell code that operates on datatypes.

In this week’s assignment, you’ll use this knowledge to implement evaluators for more interesting languages.

Background: Implementing a programming language

In this lab, you will implement a piece of a programming language. Many implementations of programming languages define the following things:

The concrete syntax, which defines the format of valid programs.
An abstract syntax, which is a data structure that represents the contents of a program.
The semantics, which defines what a program “means”. In other words, the semantics determines what happens when a program runs.

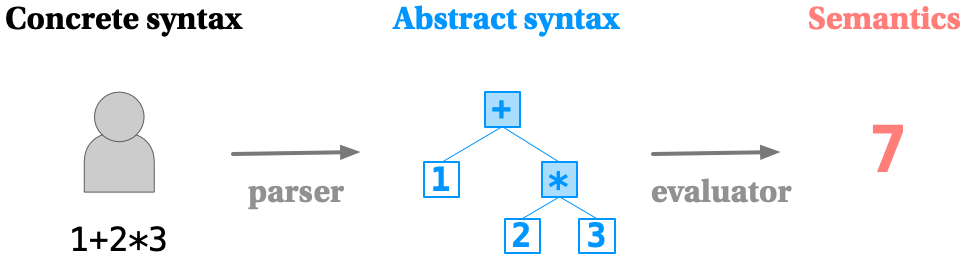
Implementation diagram — The parser translates a program from its concrete syntax to the abstract syntax. The evaluator runs the program to produce a result.

Additionally, implementations are often comprised of:

A parser to translate the concrete syntax to the abstract syntax.
An interpreter / evaluator / compiler to translate the abstract syntax to the semantics.
Some tests to make sure that the implementation works.
Some tools / environments, such as a read-eval-print loop (REPL), which help people write programs.

The code we provide you for this lab will be separated into different files, each of which is responsible for one or more of these pieces of a programming language. You’ll mainly focus on the evaluator. To do so, you’ll also need to be familiar with the abstract syntax. You can safely ignore the other pieces, if you wish.

Materials

Use the assignment workflow and the link provided on Piazza to get access to this week’s files.

If you look at the files, you’ll notice two directories: lc1 and part2. Each of these directories holds the code for a programming language:

lc1/                -- implementation of Lambda Calculus
   - AST.hs         -- the code for the abstract syntax
   - Evaluation.hs  -- the code for the evaluator
   - REPL.hs        -- the code for reading, printing, and looping
   - Main.hs        -- some sample code for running a REPL as a program
   - test/          -- a folder with code that tests the implementation

lc2/                -- implementation of Lambda Calculus, extended with some primitives
   - AST.hs         -- the code for the abstract syntax and semantic values
   - Evaluation.hs  -- the code for the evaluator
   - REPL.hs        -- the code for reading, printing, and looping
   - Main.hs        -- some sample code for running a REPL as a program
   - test/          -- a folder with code that tests the implementation

Again, you’ll be implementing the evaluator, so you’ll be most interested in the files Evaluation.hs and AST.hs.

Part 0: Warmup

To get familiar with the code, try running it in the following ways.

Run the `freeVars` function

The file lc1/Evaluation.hs contains the code for free variables that we developed in class. You can try it out in ghci.

In the lc1 directory, use ghci to load Evaluation.hs:

% ghci Evaluation.hs
GHCi, version 8.6.3: http://www.haskell.org/ghc/  :? for help
[1 of 2] Compiling AST              ( AST.hs, interpreted )
[2 of 2] Compiling Evaluation       ( Evaluation.hs, interpreted )
Ok, two modules loaded.
*Evaluation>

Try out the freeVars function on a few sample expressions:

*Evaluation> freeVars (Lambda "x" (Var "x"))
fromList []
*Evaluation> freeVars (Lambda "x" (Var "y"))
fromList ["y"]

Run the `cbn` function

The cbn function is an evaluator for our language. You can run the function using some sample expressions we’ve defined in Main.hs:

    % ghci Main.hs
    GHCi, version 8.6.3: http://www.haskell.org/ghc/  :? for help
    [1 of 4] Compiling AST              ( AST.hs, interpreted )
    [2 of 4] Compiling Evaluation       ( Evaluation.hs, interpreted )
    [3 of 4] Compiling REPL             ( REPL.hs, interpreted )
    [4 of 4] Compiling Main             ( Main.hs, interpreted )
    Ok, four modules loaded.
    *Main> cbn e1
    Lambda "x" (Apply (Var "x") (Var "x"))

Unfortunately, if you try to evaluate any expression that requires substitution, you’ll get an error. We haven’t implemented substitution yet.

Additional notes

In ghci, you can start a call-by-name REPL by running cbnREPL from Main.hs. Similarly, cbvREPL is a call-by-value REPL.
```
   *Main> cbnREPL 
   cbn> \x . x
   λx.x
```
Type quit or Control-C to quit the REPL.
In Haskell, you can parse an arbitrary lambda expression with readExpr.
```
   *Main> readExpr "lambda x . x"
   Lambda "x" (Var "x")
```
In Haskell, you can print an arbitrary lambda expression with putExpr.
```
   *Main> putExpr (Lambda "x" (Var "x"))
   λx.x
```
There are lots of provided tests you can run. See the Modules and tests page for general instructions on running tests.

Part 1: A call-by-name evaluator

Substitution

The lc1/Evaluation.hs file contains skeleton code for substitution, in the function substC.

In mathematical notation, the substitution operator is written as M[x↦N] (meaning: In lambda expression M, replace all the free xs with N.). In Haskell, we will write it in the form:

   substC targetExprM varX replacementExprN

Note, the substitution operator has the following properties (written in mathematical notation):

x[x↦N] → N (i.e., replace the variable with the thing being substituted)
y[x↦N] → y (i.e., but don’t replace other variables)
(λy.M)[x↦N] → λy.(M[x↦N]) (i.e., recurse into function bodies)
(λx.M)[x↦N] → λx.M (i.e., but not if x is a bound variable)
(L M)[x↦N] → (L[x↦N] M[x↦N]) (i.e., recurse into function applications)

Your task: Fill in the implementation for substC. You can test that it works using any of the ways described in the Warmup.

Call-by-name

Next we will use the substitution helper function to implement a lambda calculus evaluator. This technique is called “call by name” because, when we handle function application, the parameter variable in the lambda function we’re applying provides another name for an unevaluated copy of the argument expression.

If M → V then (M N) → (V N).
That is, if we have a function application, try to evaluate the function side to get it into a normal form.
((λx.M) N) → M[x↦N].
That is, if the whole expression is an anonymous function being applied to an argument, we can do the substitution.

Your task: Code is provided for cbn. If you have written substC correctly, cbn should work. But examine it to see what it does and how it works. In particular, it contains two recursive calls to cbn. Determine why each call is necessary and what the consequences would be if it were removed. You can test that it works using any of the ways described in the Warmup.

Call-by-value

Call-by-value is the same idea as call-by-name, except that to save work, rather than substituting in unevaluated arguments (which will create extra work depending on how many times they are copied), instead evaluate the argument before copying it in.

Your task: Make a small change to the cbv code to make it evaluate arguments to functions when dealing with function application. (Hint: It already evaluates the function part, you just need to make it evaluate the argument, too.) You can test that it works using any of the ways described in the Warmup.

Part 2: A more realistic language

Ideally, get this part done too, but if you don’t finish it by the end of lab, you can stop and leave this part unfinished.

Unfortunately, call-by-name and call-by-value aren’t very interesting on pure functions. (Once they have a function, they’re done. They don’t evaluate function interiors until they’re applied to something). Thus, these schemes are more interesting when we add some built-in primitives.

Look at the code in the lc2 directory (especially AST.hs and Evaluation.hs), and study the changes. Notice the addition of a Value type, and how cbn and cbv now return a Value. Once you’re comfortable with how it works, port over your code from Part 1. Test that it works using any of the ways described in the Warmup.

Part 3: Bonus fun (if you have time)

Curiously, if we removed the check on freeVars in substC, our Haskell implementation sometimes would terminate for expressions where cbv ought to infinite loop. In a comment, explain why.
Add conditional statements.
With the aid of a Y combinator, write factorial.