HW 2: Introduction to Haskell
Overview
The goal of this assignment, is to get practice with Haskell, specifically, writing functions and datatypes; using pattern-matching and recursion. We’ll also learn about stack machines, and use one to evaluate arithmetic expressions.
You may work on this assignment by yourself or with a partner. If you work with a partner, you must follow pair programming rules at all times (even when writing text or math) and share roles equally. Both members of the pair must contribute to and understand all parts of jointly submitted work. You are not required to work with your partner from lab.
Materials
Use the assignment workflow and the link provided on Piazza to get access to this week’s files.
Using your own machine
Although you should make sure that your code runs correctly on knuth, it is possible to use your own machine for this week’s assignment. To do so, you need to make sure you have Haskell and git installed. If you would like to try to set up your machine for the assignment, see this article.
Haskell: Good programming practices
The provided code generally will follow good programming practices, by adhering to a consistent style guide and documenting the code in a way that makes it easy for a tool called Haddock to autogenerate documentation.
We will also organize code into modules, which makes the code easier to test and reuse.
This week, you don’t need to worry too much about following conventions for code documentation, nor about writing and running tests. We won’t grade for style or elegance, but we will grade based on whether your code passes the tests. If you’re curious about testing, and want to learn how they work, see this article on modules and tests.
Never change the names or types of the elements in the provided code, and always adhere to the names and types described in the assignment. They constitute an interface against which we’ll test your code. If you change them, you’ll break the interface, which will cause the tests to fail. You’re free to write helper functions, unless the assignment says otherwise.
Haskell Warmup
fib [10%]
Define the Haskell function
fib :: Integer -> Integer
that computes the Fibonacci number $F_n$ when given $n\geq 0$:
\[\begin{aligned} F_0 &= 0\\ F_1 &= 1\\ F_n &= F_{n-1} + F_{n-2}\qquad\mbox{when $n\geq 2$.} \end{aligned}\]Go for simplicity over efficiency here; an exponential running-time is OK.
intfib [10%]
It is occasionally useful to consider a more general specification,
\[\begin{aligned} F_0 &= 0\\ F_1 &= 1\\ F_n &= F_{n-1} + F_{n-2}\qquad\mbox{for all integers $n$.} \end{aligned}\]Although it might not be obvious at first glance, this specification uniquely determines the value of $F_n$ for every integer $n$, not just the non-negative integers. (For example, what must $F_{-1}$ be? What about $F_{-2}$?)
Your task: Define the Haskell function
intfib :: Integer -> Integer
that computes $F_n$ for any integer $n$. Again, clarity and correctness are more important than efficiency.
Functions on lists
evens [5%]
Define the function
evens :: [a] -> [a]
that returns every other element of a list, starting with the first (zero-th).
odds [5%]
Define the function
odds :: [a] -> [a]
that returns every other element of a list starting with the second (one-th).
evenodds [5%]
Define the function
evenodds :: [a] -> ([a],[a])
such that evenodds l is the same as (evens l, odds l). Define evenodds as
its own recursive function with no calls to helper functions. You will want to
use let and pattern-matching to give names to the two lists returned by your
recursive call.
riffle [5%]
Define the function
riffle :: ([a],[a]) -> [a]
that undoes the work of evenodds, i.e., so that for any list l, the code
riffle (evenodds l) returns l. In practice, riffle will interleave the
elements of the two given lists into a single list. Make sure to document what
your function does if the lists are of different lengths.
Higher-order functions, currying and uncurrying [10%]
Background
Recall that a higher-order function is a function that takes another function as input and / or returns another function as output.
Recall also that there are two ways to define a two-argument function in Haskell. The arguments can be supplied simultaneously (as a pair) or successively (in separate applications).
For example, riffle above is supposed to take a pair of lists, i.e.,
riffle :: ([a], [a]) -> [a]
but we could have designed a slightly different interface where the two lists are supplied in succession, i.e.,
riffle2 :: [a] -> [a] -> [a]
In different circumstances, one or the other interface might be preferable. Fortunately, we can automatically convert between these two interfaces.
Your task: Define the functions
myCurry :: ( (a, b) -> c ) -> ( a -> b -> c )
myUncurry :: ( a -> b -> c ) -> ( (a, b) -> c )
that do the conversion. For example, if we define
g = myCurry f
then g x y and f (x,y) should yield the
same answer for all x and y. (In particular,
riffle2 is myCurry riffle.) Similarly, if we say
h = myUncurry k
then h (x,y) and k x y should yield the
same answer for all x and y. (In particular,
riffle is myUncurry riffle2.)
Hint: Each function can be written in a single (short) line; the code can be very trivial to write once you figure out what’s going on. Even better, there’s really only one piece of code you can write that has the correct type! So if you can read the Haskell type, you likely can write the code.
Note: The rest of the assignment makes uses of Haskell’s datatypes. We will study datatypes in detail during Wednesday’s class, so you might want to wait until Wednesday to work on the remainder of the assignment.
Haskell datatypes [8%]
Define a Haskell datatype TreeOfInt that represents a binary search tree of
Ints. This type should have two kinds of values, Empty representing an empty
tree and Branch which should store three associated values: an Int, a left
and right subtree (in that order).
Write a recursive function least that returns the minimum element of a tree (or
undefined if the tree is empty).
Evaluating arithmetic expressions using a stack machine
Background: Evaluation and stack machines
In the remainder of the assignment, we will focus on evaluating an arithmetic expression (e.g., $1 + 2 + 3$), reducing it to single value (e.g., $6$). To reduce an expression to a value, we first need a representation: a data structure that we can use to store information about the expression. We then need an evaluator: an algorithm that takes the representation as input and produces the result as output.
We’ll focus mainly on stack-machines: a way to use a stack to evaluate an expression. Along the way, we’ll see how Haskell’s datatypes and pattern matching provide a clear and concise way to implement evaluators.
Background: Tree- and list-based representations for arithmetic expressions
One way to represent arithmetic expressions is as a tree. The interior nodes are operations (e.g., addition, subtraction, etc.), and the leaves are numbers.
Consider these datatypes for representing arithmetic expressions:
data Expr = Num Double
| BinOp Expr Op Expr
deriving (Show, Eq)
data Op = PlusOp | MinusOp | TimesOp | DivOp
deriving (Show, Eq)
Using these datatypes, the mathematical expression $(2+3)*7$ is represented in Haskell like so:
BinOp (BinOp (Num 2) PlusOp (Num 3)) TimesOp (Num 7)
In contrast, certain calculators and programming languages evaluate expressions using a stack. An arithmetic computation is a list of stack instructions. We can represent stack instructions with this datatype:
data StackInstr = Push Double
| DoOp Op
| Swap
deriving (Show, Eq)
The instruction Push r means “push the number $r$ onto the stack”;
the instructions DoOp PlusOp, DoOp MinusOp, DoOp TimesOp, and
DoOp DivOp mean “replace the top two numbers on the stack with
their sum”, “… their difference”, and so forth. The Swap
instruction means “swap the top two numbers on the stack”. In summary:
| If the stack looks like | and the operation is | afterwards the stack should be |
|---|---|---|
| … | Push $r$ |
$r$ … |
| $a$ $b$ … | DoOp PlusOp |
$(b+a)$ … |
| $a$ $b$ … | DoOp MinusOp |
$(b-a)$ … |
| $a$ $b$ … | DoOp TimesOp |
$(b*a)$ … |
| $a$ $b$ … | DoOp DivOp |
$(b/a)$ … |
| $a$ $b$ … | Swap |
$b$ $a$ … |
Note: In this diagram, the top of the stack is shown on the left.
Using this datatype, the mathematical expression $(2+3)*7$ is represented in Haskell like so:
[Push 2, Push 3, DoOp PlusOp, Push 7, DoOp TimesOp]
Stack evaluation [10%]
Now we will implement a stack-based evaluator. The evaluator will take as input an expression represented as a list of stack instructions. It will then use a stack to reduce the expression to a single value. We will represent the stack as a list of floating-point numbers:
type StackValue = Double
type Stack = [StackValue]
The head of the list corresponds to the top of the stack.
Your task: To implement an evaluator, write a recursive function
evalRPN :: [StackInstr] -> Stack -> StackValue
that takes two inputs—a list of stack instructions and a stack, uses the stack to perform the stack operations in order, and returns the number at the top of the stack. Here is an example:
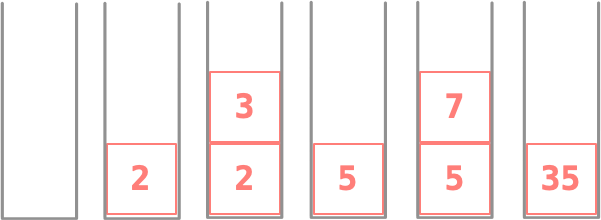
[Push 2, Push 3, DoOp PlusOp, Push 7, DoOp TimesOp], we evaluate each instruction in turn, which causes the stack to change.
Be careful to get the order right for MinusOp and DivOp. For
example,
evalRPN [Push 2.0, Push 1.0, DoOp MinusOp] []
should return 1.0, not -1.0.
Don’t worry about performance or runtime errors
For this and subsequent problems on the assignment, don’t worry about inefficiency caused by
repeated list-appends (++). Also, your code does not need to handle stack underflow (stack
operations executed without enough values on
the stack) or other run-time errors.
Translating from a tree-based representation to stack operations [10%]
Write a function
toRPN :: Expr -> [StackInstr]
that converts an arithmetic expression (represented as a tree) to a list of stack
operation instructions that computes the same expression. There
should be a DoOp PlusOp stack operation for every PlusOp in
the input, and so on; evaluating the input expression to a
number $r$ and then returning [Push r] is not acceptable.
Background: Minimizing the stack depth
Warning: this part requires serious thought before you start coding!
The same arithmetic expression can be computed in several ways
using the stack machine. For each subexpression, you can choose
to evaluate the left side first or the right side first. Because
subtraction and division are not commutative, evaluating the
right side before the left requires a Swap to fix things
up.
Note: There would be even more possibilities if we permit reassociation, e.g., computing $(a+b)+(c+d)$ as $a+(b+(c+d))$. Unfortunately, floating-point arithmetic is not associative in general (because floating-point errors accumulate in a way that depends on the order of operations), so reassociation might change the answer. Thus, for this problem you should only consider the choice of evaluating each operator by doing either the left subexpression first or the right subexpression first.
For example, $1.0 - (2.0 + 3.0)$ can be computed either by the sequence
[Push 1.0, Push 2.0, Push 3.0, DoOp PlusOp, DoOp MinusOp]
or by
[Push 2.0, Push 3.0, DoOp PlusOp, Push 1.0, Swap, DoOp MinusOp]
The first list of instructions requires a stack that can hold at least three numbers simultaneously, whereas the second list never requires more than two numbers on the stack at any one time. This figure illustrates the difference:

toRPNopt [20%]
Define the function
toRPNopt :: Expr -> ([StackInstr], Integer)
that returns a pair containing (1) an optimal sequence of operations to evaluate the given arithmetic expression, and (2) the maximum number of values simultaneously on the stack during the execution of this sequence. Optimal here is defined to mean “requiring the smallest amount of stack space to evaluate”, which means having the smallest maximum number of values on the stack at once.
Implementation notes
-
This function can be computed inductively, using the optimal instruction sequence for the first operand, the optimal sequence for the second operand, and the stack sizes they each require.
-
You can decide whether to evaluate the left side first or the right side first just by looking at the stack depth that each side requires (and without looking at the particular operations!). Do not write a separate helper function that does nothing but compute stack depths.
-
You can use pattern-matching and
let...insyntax to give names to the two values returned by each recursive call.
Example expressions [2%]
Define two specific, tree-based representations of arithmetic expressions (i.e,
valid inputs for toRPN and toRPNopt)
depth3 :: Expr
depth4 :: Expr
that require maximum stack depth 3 and 4 respectively, even when taking
optimal advantage of commutativity. That is, when fed into a correct
implementation of toRPNopt, these expressions should report the
best achievable stack depth to be 3 and 4 respectively.
Where to go from here
In this assignment, we focused on using a data structure to represent a program. For example, we used a list of stack operations to represent an arithmetic expression. The idea that we can represent programs as structured data is a powerful one, and one of the central ideas of this course. We will revisit and build on this idea several times this semester.
The Haskell programming language, is an ideal language for studying the idea of programs-as-structured-data. With its datatypes and pattern matching, Haskell gives us an expressive and succinct way to represent and operate over structured data that takes different forms.
After completing the assignment, if you are interested in further exploring these ideas, consider the following:
- What if we wanted to introduce the idea of “memory” to our stack evaluator? For
example, what if we wanted to add commands that could store and recall the result of a
computation? How would we need to change our
StackInstrdata type? How would we need to change our evaluator? - How might we write a
fromRPNfunction that converts a list of stack operations to the corresponding arithmetic expression?